| 1. | Introduction |
| 2. | Rethinking Algorithm Animations... |
| 3. | System Architecture |
| 4. | Experiments with Hypermedia Algorithm Visualization |
| 5. | Conclusion |
| 6. | References |
| 7. | Acknowledgements |
![]()
Helping Learners
Visualize and Comprehend Algorithms*
Steven
R. Hansen, Air Command and Staff College
N. Hari Narayanan, Auburn
University
Dan Schrimpsher, Teledyne
Brown Engineering
Abstract
The idea
of using animations to illustrate dynamic behaviors of computer algorithms
is over fifteen years old. Over a hundred algorithm animation systems
have been built since then, with most developed in the belief that the
animations would serve as effective learning aids for students. However,
only recently have researchers started asking the question do algorithm
animations really help? Unfortunately, results of experiments driven by
this question have been disappointing. We believe that previous attempts
at using animation to teach algorithm behavior were unsatisfactory not
because of a flaw with animation as a technique, but because of the approach
used to convey the animations. This paper provides an overview of our
algorithm visualization research, based on the premise that a rethinking
of algorithm animation design is required in order to harness its power
to enhance learning. A novel theoretical framework for the design of effective
algorithm visualizations, one which espouses embedding interactive analogies
and animations in hypermedia to enhance contextual learning, is presented
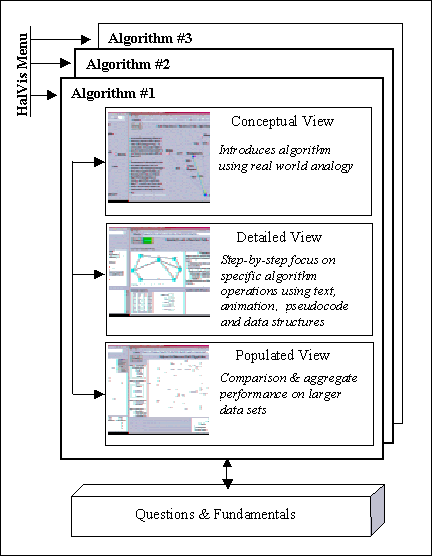
first. We then describe the architecture of HalVis, an implemented system
based on this framework, and illustrate the various learning components
of this architecture through an annotated slideshow of a visualization
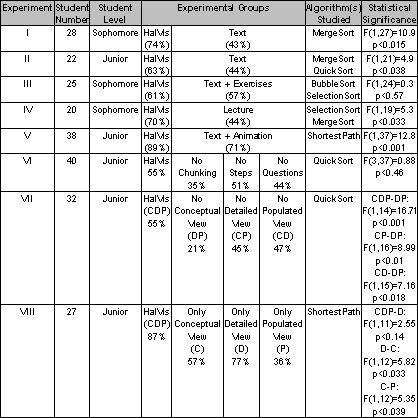
of the SelectionSort algorithm. Finally, a summary of results from eight
empirical studies conducted over three years, involving more than 230
undergraduate students, is provided. These experiments demonstrated a
statistically significant advantage of our framework over both traditional
means of instruction and algorithm animations representative of extant
research on this topic. They also led to a surprising discovery of the
important role of interactive and animated analogies in priming learning
about algorithms from subsequent visualizations.
![]()