
The Logic Tutor: A Multimedia Presentation
David
Abraham, University of Sydney
Liz Crawford, University
of Sydney
Leanna Lesta, University
of Sydney
Agathe Merceron, University
of Sydney
Kalina Yacef, University
of Sydney
About
the authors...
Abstract
This paper presents
the Logic Tutor, a tool to support computer science students in their learning
of logic and more specifically in their learning of formal proofs. The current
tool is equipped with a deduction system for propositional logic, with a modular
design that makes it easy to change to another logic. Preliminary evaluation
shows that this tool has a high educational value, thanks, among other features,
to its simple, attractive interface, and its highly specific error messages.
The Logic Tutor is integrated into our Logic teaching course as of 2001.
1. Introduction
For a few decades
now, computers have played an increasing role in education. They provide a more
or less personalised environment where the learners can practice at their own
pace, have access to tutorial lessons, be given explanations and feedback on
their performance and so on. Intelligent Tutoring Systems, which make use of
findings in Artificial Intelligence and Cognitive Science, are a popular target,
but also require a lot more effort to build. On the other hand, non-intelligent
but well-designed systems can also be educationally excellent (du Boulay 2000,
Gugerty & Hicks 1993). Dugdale emphasizes (in Dugdale 1992) the benefit
of using simple computer-based tutors in mathematics which are able to provide
feedback step-by-step. However, although well designed, these programs are not
"intelligent" in the sense that they do not provide individualized
instruction. The system presented in this paper, the Logic Tutor, addresses
this shortcoming. It is a well-designed program with an attractive interface.
Additionally, it has basic intelligent features such as the expertise to apply
rules of inference and laws of equivalence, as well as a level of adaptability
to the user.
Propositional logic is a fundamental topic in computer science and mathematics (Merceron 2001). When studying formal logic, students learn how conclusions can be validly derived from a set of premises using logical rules. The concept of formal proof is not easy for students to understand, and the best way to grasp it is through exercises. However exercises are beneficial only with feedback. Students have to know whether they are right or wrong, and, when they are wrong, they have to know what is wrong and be given a chance to try again. But the increasing number of students in computer science makes it difficult to provide enough human tutors to assist students in this part of their learning.
Computers themselves can help with this problem. Formal proofs, by their very nature of being formal, can be automated. This means also that computer programs can check formal proofs given by students. Thus, formal logic is an excellent topic to be presented by means of computer-based tutorials.
Existing tools for practicing logic have not matched our expectations, mainly because their GUIs were not attractive enough and they had high barriers to initial use. This led us to design our own tool. The Logic Tutor presents exercises of formal proofs in propositional logic, checks students' answers, and provides feedback. It has been developed with an emphasis on educational value.
Educational value in the Logic Tutor is achieved by five means. First the Logic Tutor provides step by step feedback. Each time a student enters a line of the proof, the line is checked for correctness. In case of a mistake, extensive explanation is provided by the use of a 'cascading mistakes' principle (See the multimedia presentation in section 2.1). Second, several levels of help are provided, ranging from a quick start button, to a handy reference to rules of inference, to a tutorial on proof strategies. Third, the "history" feature provides students not only with the exercises they have done or attempted, but also with statistics on their mistakes. Fourth, files of exercises may be easily created with a possibility of comments, hints, and partial or even complete solutions. And lastly, the Logic Tutor has a simple and attractive graphical interface. This simplicity helps to eliminate the barriers to student learning.
1.1 A Typical Session
with the Logic Tutor
Let us first provide an overview of a typical session with the Logic Tutor.
The video demonstration we have prepared shows:
![]() A screenshot movie (~550 KB) for the demonstration.
A screenshot movie (~550 KB) for the demonstration.
2. Description of the
Tool
The Logic Tutor is written
in Java, which makes it a portable tool. It has a modular design. The main modules
are the user interface module, the student module, and the logical system module.
The interface module makes use of the Java Swing library. The student module
stores information specific to the student's use of the tool. It records all
the attempted exercises along with mistakes. The logical system module is divided
into two sub-modules, the verification module and the mistake module. The verification
module has the logic expertise and checks the correctness of a student's deductions.
The mistake module is articulated to a database of mistake patterns, which is
used to produce proper feedback when a student error occurs. This modular design
makes it easy to change the logic, as only a few classes are affected. The plug-in
of another logic has been successfully tested.
Figure 1 gives a snapshot of the main screen of the tool. The background window provides the main buttons on the top, including the help button. Buttons giving access to user-specific information are on the right. The screen is mainly filled by the table showing the deduction so far, which constitutes the background of Figure 1. The student enters a new line of deduction at the bottom of the screen. All parts of a deduction line are clearly separated. Colours are used to enhance readability of formulas: brackets are red, operators are blue, while propositions are black. The window in the middle of the screen presents an exercise. The premises and the conclusion are listed on separate lines. The lecturer may use the comment below the exercise to give an instruction. The exercise shown in Figure 1 should be solved using an indirect proof first, which in this case is short. Then a direct proof may be attempted.
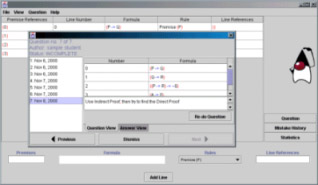
Figure 1. Snapshot of the screen when a new question to solve is currently loaded.
2.1 Handling of Mistakes
One of the requirements that we specified for our Logic Tutor was to provide
quality feedback to users when they make mistakes. To achieve this requirement,
each logical system, presently the propositional logic system, stores a database
of mistake patterns. Whenever the student uses a rule incorrectly, the mistake
database is interrogated to find the type of mistake made. The mistake viewer
displays in black the mistake made and in blue the hint given to the students.
The Java code that checks for mistakes when deductions are entered is thus independent
of the logical system the student is currently operating.
When students make mistakes, they have quite often made more than one error. This leads to the principle of cascading mistakes. First it is checked that all the fields in the answer are filled with the right type of data. Then the formula is checked for its syntax. In case of a mistake, the parser provides good error messages. Then the real cascade in the derivation begins. The lower level represents general mistakes like incorrect line number and invalid application of the rule. The next level is when the expert module detects that the rule specified by the user can be applied, using lines other than those provided by the user. Then the next level is for cases where the rule specified by the user cannot be applied but where another one can be applied with the same lines provided by the user. The higher level of mistakes deals with more specific mistakes, like the use of Simplification without Commutation to deduce the right hand side of a conjunct. A clear illustration of the principle of cascading mistake can be found here.
![]() A Powerpoint file (~120 KB) or a ppz
file (~83 KB) available for download.
A Powerpoint file (~120 KB) or a ppz
file (~83 KB) available for download.
All mistakes are context sensitive, which means that explanations are adjusted to the current exercise.
A careful analysis of mistakes made by the students led to the organisation of the database mistakes according to patterns. Currently the database has 50 patterns. Two patterns are given as examples below.
Incorrect Justification Pattern: The mistake-analyzer looks at the deduction and can determine that the user meant to use, say, Commutation, but confused the name with Association.
Incorrect Line of Reference Pattern: The mistake analyzer picks up typing errors when the user enters the line number references. It will inform them of the correct line numbers by printing "Try using (1, 3) instead", for example.
2.2 Help
The quick start guide provides
the user with explanations on the basic functionalities of the Logic Tutor such
as logging in, selecting an exercise, using the exercise viewer, entering deductions,
and reviewing mistakes and statistics.
Proof strategies give hints on how to start a proof. Strategies are organised by the form of the conclusion following the usual syntax of propositional formulas: atomic formulas, negated formulas, and-formulas, or-formulas, conditional formulas and bi-conditional formulas.
Rules of inference and laws of equivalence are handy overview tables.
2.3 User History
The module history records every exercise the student attempts. It is worth
noticing that not summaries of exercises but exercise objects themselves are
stored. This means that mistakes made and comments written by students are also
stored. This extra functionality gives many benefits. First, students are able
to continue unfinished exercises and redo exercises. Second, in the weeks before
the exam, students can navigate their entire history for revision. Finally,
the Logic Tutor can generate a report card, which includes statistics on each
type of mistakes, how often each rule is used, and much more.
2.4 Exercise Files
The ability to store exercise objects allows tutors and lecturers to create
files of exercises that can be distributed to students. It is possible to associate
comments with exercises and there are many uses for this. A comment can describe
the difficulty of a question. It can provide a hint like "use modus ponens".
It can provide a restriction like "Try to do without commutation'' or simply
give instructions like "Do this using indirect proof." This latter ability is
shown in Figure 1. Furthermore, once students have loaded the file, they may
annotate the comments. Finally, exercises may be provided with partial or complete
solutions.
2.5 User Interface
The graphical user interface is extremely important. It has to be both simple
and attractive; otherwise, students will not use the tool. The GUI of the Logic
Tutor has a tabular view. Thus it is possible for a user to adjust the width
of each column and even to change the order of the columns. The GUI uses coloured
text, which makes the reading of formulas easier. Each symbol type has its specific
colour, as is shown in Figure 1. A changeable look and feel has been implemented
in the View menu so that users can adapt the look and feel to what they are
comfortable with. For example, users who learn this program on a Unix machine
at their university and then occasionally take it home to their Windows machine
can change the program to look like a Unix program - even when they are using
Windows.
2.6 Exercise Generator
The Logic Tutor has been
expanded with a tool that generates exercises for the lecturer based on certain
criteria the lecturer sets for a problem. First the lecturer sets weights to
the rules. Rules with a high weight should be used to solve the generated exercise,
while rules with a low weight may be used, but should not necessarily be used
in the solution. The lecturer provides also a set of premises to start with.
This gives a better chance to generate interesting exercises. Finally the lecturer
sets the length of the exercises, which is the number of steps needed to derive
the conclusion. The greater the length, the more difficult the exercise. The
tool uses a forward chaining algorithm that selects rules at random from the
weighted set to make inferences starting with the premises. The formula reached
after the length specified for the derivation becomes the conclusion of the
exercise. That way, not only an exercise but also a solution is generated.
For example if the lecturer enters the following premises:
(A | (B -> D))
(~C -> (D -> E))
(D & (B | C))
(A -> C)
~C
The Exercise Generator will produce the following exercises:
|
Premises:
Conclusion: (B -> E) |
Premises:
Conclusion: E |
….. |
In practice, not all exercises generated by the tool are considered interesting by the lecturer. Nonetheless, many exercises are generated so that the lecturer is left with enough material to train the students in the use of specific rules.
3. Preliminary Evaluation
The tool was qualitatively evaluated last year and this year on a voluntary
basis by students who took the Logic course last year and by tutors. In total
14 people participated in the preliminary evaluation (Later this year (November
2001) a full evaluation will be conducted with the 450 students enrolled in
the course). The evaluation consisted in a one-hour session on the Logic Tutor
without external help, followed by a questionnaire. Each question addressed
a feature of the Logic Tutor or a broader aspect of its use. People were asked
to range their level of satisfaction between 1 (lowest) and 5 (highest) and
the graphs below show the weighted percentage of satisfaction. All students
and tutors are unanimous in saying that the tool is a very useful learning tool
(answers were all above 4). The graphs below (Figures 2 and 3) show that the
interface encouraged people to use the program (87% of satisfaction); 90% found
it easy to use and to do what they wanted it to do. Users strongly agreed (97%)
that the Logic Tutor is useful from a learning point of view. Interestingly,
users were divided over the need for handling other types of Logic (such as
predicate logic). Reading from their comments, the Logic Tutor helps people
to grasp the mechanism for conducting formal proofs. Once it is acquired, the
benefit of practicing on predicate logic is not as important.
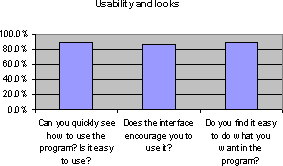
Figure 2. Evaluation results for usability and looks

Figure 3. Evaluation results for Course involvement
The users' positive comments were that the Logic Tutor is a very useful learning tool, allowing students to practice at their own pace and as often as they want, providing very appropriate error messages and useful hints.
The evaluation survey also questioned the users about shortcomings of the system. Some minor problems such as the display of the conclusion while doing an exercise and the ability of opening several windows were mentioned. The most obvious suggestions were added to the system accordingly.
4. Conclusion
Summing up, the Logic Tutor
is a tool to support students in their learning of formal logic, and more specifically
formal proofs. It cannot yet be classified as an intelligent tutor. However,
it has intelligent characteristics. It possesses an expert module that enables
it to apply rules of inference and laws of equivalence of propositional logic.
Expert modules constitute the foundation of any intelligent tutor (Anderson
1988). Moreover its feedback takes into account the input of the user, and,
in many cases, the explanations provided are as enlightening as the ones provided
by a good human tutor.
Immediate future work includes modifying the present tool according to the results of the preliminary evaluation to increase users' comfort.
We are also working on a Teacher Assistant System (Yacef 2000), which will embed:
This will improve even more the educational value of the tool, both for the student and for the lecturer.
Finally, our aim is to increase the multimedia aspect of this course to encourage flexible and independent learning. Our logic course has been redesigned this year to include this tool at the teaching, training and assessment levels. It includes more media, like a set of commented solutions accessible from the web. Tutors have written commented solutions after watching mistakes made and difficulties encountered by students while solving exercises. Comments include traps to avoid and hints to find solutions. The course evaluation last year has shown that students find them very valuable.
5. Acknowledgements
The authors thank Rainer Wasinger for conducting the preliminary evaluation
and all the volunteers and tutors who agreed to spend some time evaluating our
tool.
6. References
Anderson, J.R. (1988). The
expert module. In Foundations of intelligent tutoring systems, M.C. Polson
& J.J Richardson, eds Hillsdale: NJ: Lawrence Erlbaum Associates, pp. 21-53.
Du Boulay, B. (2000). Can we learn from ITSs ?, Invited talk at the 5th International Conference on Intelligent Tutoring Systems, Montreal, June 2000.
Dugdale, S. (1992) The design of computer-based mathematics education. In Computer-Assisted Instruction and Intelligent Tutoring Systems: shared goals and complementary approaches. J.H Larkinand R.W Chabay, eds. Lawrence Erlbaum, pp. 11-45.
Greer J. & McCalla, G. (1994). Student Modelling, the key to individualised knowledge-based instruction. Berlin, Springer-Verlag.
Gugerty, L. & Hicks, K. (1993), Non-diagnostic intelligent tutoring systems, Proceedings of the 15th interservice/industry training systems and education conference. Orlando, Florida, pp. 450-459.
Kay, J.(1997). Learner know thyself : student models to give learner control and responsibility. Keynote address at ICCE'97, Kuching.
Merceron, A. (2001). Languages and Logic. Pearson Education Australia.
Yacef, K. (1999) Towards an intelligent instructor-assistant system for training operators of complex and dynamic skills. Ph.D. Dissertation. University of Paris 5 and INRIA.
Yacef, K. (2000). Providing an intelligent tutoring aid to assist undergraduate teaching. SESQUI Internal proposal report, University of Sydney, Sydney, Australia.
********** End of Document **********
| IMEJ multimedia team member assigned to this paper | Yue-Ling Wong |