Printer friendly version

The Logic Tutor: A Multimedia Presentation
David Abraham, University of Sydney
Liz Crawford, University of Sydney
Leanna Lesta, University of Sydney
Agathe Merceron, University of Sydney
Kalina Yacef, University of Sydney

Abstract
This paper presents the Logic Tutor, a tool to support computer science students in their learning of logic and more specifically in their learning of formal proofs. The current tool is equipped with a deduction system for propositional logic, with a modular design that makes it easy to change to another logic. Preliminary evaluation shows that this tool has a high educational value, thanks, among other features, to its simple, attractive interface, and its highly specific error messages. The Logic Tutor is integrated into our Logic teaching course as of 2001.

1. Introduction
For a few decades now, computers have played an increasing role in education. They provide a more or less personalised environment where the learners can practice at their own pace, have access to tutorial lessons, be given explanations and feedback on their performance and so on. Intelligent Tutoring Systems, which make use of findings in Artificial Intelligence and Cognitive Science, are a popular target, but also require a lot more effort to build. On the other hand, non-intelligent but well-designed systems can also be educationally excellent (du Boulay 2000, Gugerty & Hicks 1993). Dugdale emphasizes (in Dugdale 1992) the benefit of using simple computer-based tutors in mathematics which are able to provide feedback step-by-step. However, although well designed, these programs are not "intelligent" in the sense that they do not provide individualized instruction. The system presented in this paper, the Logic Tutor, addresses this shortcoming. It is a well-designed program with an attractive interface. Additionally, it has basic intelligent features such as the expertise to apply rules of inference and laws of equivalence, as well as a level of adaptability to the user.

Propositional logic is a fundamental topic in computer science and mathematics (Merceron 2001). When studying formal logic, students learn how conclusions can be validly derived from a set of premises using logical rules. The concept of formal proof is not easy for students to understand, and the best way to grasp it is through exercises. However exercises are beneficial only with feedback. Students have to know whether they are right or wrong, and, when they are wrong, they have to know what is wrong and be given a chance to try again. But the increasing number of students in computer science makes it difficult to provide enough human tutors to assist students in this part of their learning.

Computers themselves can help with this problem. Formal proofs, by their very nature of being formal, can be automated. This means also that computer programs can check formal proofs given by students. Thus, formal logic is an excellent topic to be presented by means of computer-based tutorials.

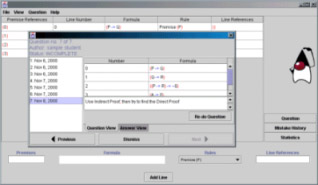
Existing tools for practicing logic have not matched our expectations, mainly because their GUIs were not attractive enough and they had high barriers to initial use. This led us to design our own tool. The Logic Tutor presents exercises of formal proofs in propositional logic, checks students' answers, and provides feedback. It has been developed with an emphasis on educational value.

Educational value in the Logic Tutor is achieved by five means. First the Logic Tutor provides step by step feedback. Each time a student enters a line of the proof, the line is checked for correctness. In case of a mistake, extensive explanation is provided by the use of a 'cascading mistakes' principle (See the multimedia presentation in section 2.1). Second, several levels of help are provided, ranging from a quick start button, to a handy reference to rules of inference, to a tutorial on proof strategies. Third, the "history" feature provides students not only with the exercises they have done or attempted, but also with statistics on their mistakes. Fourth, files of exercises may be easily created with a possibility of comments, hints, and partial or even complete solutions. And lastly, the Logic Tutor has a simple and attractive graphical interface. This simplicity helps to eliminate the barriers to student learning.

About the authors...

1.1 A Typical Session with the Logic Tutor
Let us first provide an overview of a typical session with the Logic Tutor. The video demonstration we have prepared shows:

• the running of an exercise, where the user enters formulae sequentially to prove the argument given the premises.
• the feedback received when the student makes two mistakes.
• the final feedback received when the student completes the exercise.
• the student selecting the user statistics window, to see the percentage of mistakes made per rules.

A screenshot movie (~550 KB) for the demonstration.

2. Description of the Tool
The Logic Tutor is written in Java, which makes it a portable tool. It has a modular design. The main modules are the user interface module, the student module, and the logical system module. The interface module makes use of the Java Swing library. The student module stores information specific to the student's use of the tool. It records all the attempted exercises along with mistakes. The logical system module is divided into two sub-modules, the verification module and the mistake module. The verification module has the logic expertise and checks the correctness of a student's deductions. The mistake module is articulated to a database of mistake patterns, which is used to produce proper feedback when a student error occurs. This modular design makes it easy to change the logic, as only a few classes are affected. The plug-in of another logic has been successfully tested.

Figure 1 gives a snapshot of the main screen of the tool. The background window provides the main buttons on the top, including the help button. Buttons giving access to user-specific information are on the right. The screen is mainly filled by the table showing the deduction so far, which constitutes the background of Figure 1. The student enters a new line of deduction at the bottom of the screen. All parts of a deduction line are clearly separated. Colours are used to enhance readability of formulas: brackets are red, operators are blue, while propositions are black. The window in the middle of the screen presents an exercise. The premises and the conclusion are listed on separate lines. The lecturer may use the comment below the exercise to give an instruction. The exercise shown in Figure 1 should be solved using an indirect proof first, which in this case is short. Then a direct proof may be attempted.

2.1 Handling of Mistakes
One of the requirements that we specified for our Logic Tutor was to provide quality feedback to users when they make mistakes. To achieve this requirement, each logical system, presently the propositional logic system, stores a database of mistake patterns. Whenever the student uses a rule incorrectly, the mistake database is interrogated to find the type of mistake made. The mistake viewer displays in black the mistake made and in blue the hint given to the students. The Java code that checks for mistakes when deductions are entered is thus independent of the logical system the student is currently operating.

When students make mistakes, they have quite often made more than one error. This leads to the principle of cascading mistakes. First it is checked that all the fields in the answer are filled with the right type of data. Then the formula is checked for its syntax. In case of a mistake, the parser provides good error messages. Then the real cascade in the derivation begins. The lower level represents general mistakes like incorrect line number and invalid application of the rule. The next level is when the expert module detects that the rule specified by the user can be applied, using lines other than those provided by the user. Then the next level is for cases where the rule specified by the user cannot be applied but where another one can be applied with the same lines provided by the user. The higher level of mistakes deals with more specific mistakes, like the use of Simplification without Commutation to deduce the right hand side of a conjunct. A clear illustration of the principle of cascading mistake can be found here.

A Powerpoint file (~120 KB) or a ppz file (~83 KB) available for download.

2.2 Help
The quick start guide provides the user with explanations on the basic functionalities of the Logic Tutor such as logging in, selecting an exercise, using the exercise viewer, entering deductions, and reviewing mistakes and statistics.

Proof strategies give hints on how to start a proof. Strategies are organised by the form of the conclusion following the usual syntax of propositional formulas: atomic formulas, negated formulas, and-formulas, or-formulas, conditional formulas and bi-conditional formulas.

Rules of inference and laws of equivalence are handy overview tables.

2.3 User History
The module history records every exercise the student attempts. It is worth noticing that not summaries of exercises but exercise objects themselves are stored. This means that mistakes made and comments written by students are also stored. This extra functionality gives many benefits. First, students are able to continue unfinished exercises and redo exercises. Second, in the weeks before the exam, students can navigate their entire history for revision. Finally, the Logic Tutor can generate a report card, which includes statistics on each type of mistakes, how often each rule is used, and much more.

2.4 Exercise Files
The ability to store exercise objects allows tutors and lecturers to create files of exercises that can be distributed to students. It is possible to associate comments with exercises and there are many uses for this. A comment can describe the difficulty of a question. It can provide a hint like "use modus ponens". It can provide a restriction like "Try to do without commutation'' or simply give instructions like "Do this using indirect proof." This latter ability is shown in Figure 1. Furthermore, once students have loaded the file, they may annotate the comments. Finally, exercises may be provided with partial or complete solutions.

2.5 User Interface
The graphical user interface is extremely important. It has to be both simple and attractive; otherwise, students will not use the tool. The GUI of the Logic Tutor has a tabular view. Thus it is possible for a user to adjust the width of each column and even to change the order of the columns. The GUI uses coloured text, which makes the reading of formulas easier. Each symbol type has its specific colour, as is shown in Figure 1. A changeable look and feel has been implemented in the View menu so that users can adapt the look and feel to what they are comfortable with. For example, users who learn this program on a Unix machine at their university and then occasionally take it home to their Windows machine can change the program to look like a Unix program - even when they are using Windows.

2.6 Exercise Generator
The Logic Tutor has been expanded with a tool that generates exercises for the lecturer based on certain criteria the lecturer sets for a problem. First the lecturer sets weights to the rules. Rules with a high weight should be used to solve the generated exercise, while rules with a low weight may be used, but should not necessarily be used in the solution. The lecturer provides also a set of premises to start with. This gives a better chance to generate interesting exercises. Finally the lecturer sets the length of the exercises, which is the number of steps needed to derive the conclusion. The greater the length, the more difficult the exercise. The tool uses a forward chaining algorithm that selects rules at random from the weighted set to make inferences starting with the premises. The formula reached after the length specified for the derivation becomes the conclusion of the exercise. That way, not only an exercise but also a solution is generated.

For example if the lecturer enters the following premises:

(A | (B -> D))
(~C -> (D -> E))
(D & (B | C))
(A -> C)
~C

 

Premises: (A -> C) (A | (B -> D)) (~C -> (D -> E)) ~C Conclusion: (B -> E)

Premises: (D & (B | C)) ~C (~C -> (D -> E)) Conclusion: E

…..

In practice, not all exercises generated by the tool are considered interesting by the lecturer. Nonetheless, many exercises are generated so that the lecturer is left with enough material to train the students in the use of specific rules.

3. Preliminary Evaluation
The tool was qualitatively evaluated last year and this year on a voluntary basis by students who took the Logic course last year and by tutors. In total 14 people participated in the preliminary evaluation (Later this year (November 2001) a full evaluation will be conducted with the 450 students enrolled in the course). The evaluation consisted in a one-hour session on the Logic Tutor without external help, followed by a questionnaire. Each question addressed a feature of the Logic Tutor or a broader aspect of its use. People were asked to range their level of satisfaction between 1 (lowest) and 5 (highest) and the graphs below show the weighted percentage of satisfaction. All students and tutors are unanimous in saying that the tool is a very useful learning tool (answers were all above 4). The graphs below (Figures 2 and 3) show that the interface encouraged people to use the program (87% of satisfaction); 90% found it easy to use and to do what they wanted it to do. Users strongly agreed (97%) that the Logic Tutor is useful from a learning point of view. Interestingly, users were divided over the need for handling other types of Logic (such as predicate logic). Reading from their comments, the Logic Tutor helps people to grasp the mechanism for conducting formal proofs. Once it is acquired, the benefit of practicing on predicate logic is not as important.

The users' positive comments were that the Logic Tutor is a very useful learning tool, allowing students to practice at their own pace and as often as they want, providing very appropriate error messages and useful hints.

The evaluation survey also questioned the users about shortcomings of the system. Some minor problems such as the display of the conclusion while doing an exercise and the ability of opening several windows were mentioned. The most obvious suggestions were added to the system accordingly.

4. Conclusion
Summing up, the Logic Tutor is a tool to support students in their learning of formal logic, and more specifically formal proofs. It cannot yet be classified as an intelligent tutor. However, it has intelligent characteristics. It possesses an expert module that enables it to apply rules of inference and laws of equivalence of propositional logic. Expert modules constitute the foundation of any intelligent tutor (Anderson 1988). Moreover its feedback takes into account the input of the user, and, in many cases, the explanations provided are as enlightening as the ones provided by a good human tutor.

Immediate future work includes modifying the present tool according to the results of the preliminary evaluation to increase users' comfort.

We are also working on a Teacher Assistant System (Yacef 2000), which will embed:

• The Logic Tutor, as described in this paper, with a proper learner model, i.e. with insight in the knowledge level and difficulties of the student. This learner model uses MOST, a skill acquisition model (Yacef 1999) and maintains the present "scrutability" as it can help the learner to learn better (Greer & McCalla 1994, Kay 1997).
• The Teacher's module of the Logic Tutor, whose role is to upstream the information gathered from the students' interactions with the Logic Tutor to the teaching team. The lecturer for example can visualise the results of the class and adapt his/her teaching accordingly.

5. Acknowledgements
The authors thank Rainer Wasinger for conducting the preliminary evaluation and all the volunteers and tutors who agreed to spend some time evaluating our tool.

6. References
Anderson, J.R. (1988). The expert module. In Foundations of intelligent tutoring systems, M.C. Polson & J.J Richardson, eds Hillsdale: NJ: Lawrence Erlbaum Associates, pp. 21-53.

Du Boulay, B. (2000). Can we learn from ITSs ?, Invited talk at the 5th International Conference on Intelligent Tutoring Systems, Montreal, June 2000.

Dugdale, S. (1992) The design of computer-based mathematics education. In Computer-Assisted Instruction and Intelligent Tutoring Systems: shared goals and complementary approaches. J.H Larkinand R.W Chabay, eds. Lawrence Erlbaum, pp. 11-45.

Greer J. & McCalla, G. (1994). Student Modelling, the key to individualised knowledge-based instruction. Berlin, Springer-Verlag.

Gugerty, L. & Hicks, K. (1993), Non-diagnostic intelligent tutoring systems, Proceedings of the 15th interservice/industry training systems and education conference. Orlando, Florida, pp. 450-459.

Kay, J.(1997). Learner know thyself : student models to give learner control and responsibility. Keynote address at ICCE'97, Kuching.

Merceron, A. (2001). Languages and Logic. Pearson Education Australia.

Yacef, K. (1999) Towards an intelligent instructor-assistant system for training operators of complex and dynamic skills. Ph.D. Dissertation. University of Paris 5 and INRIA.

Yacef, K. (2000). Providing an intelligent tutoring aid to assist undergraduate teaching. SESQUI Internal proposal report, University of Sydney, Sydney, Australia.

********** End of Document **********

IMEJ multimedia team member assigned to this paper	Yue-Ling Wong