

Interaction Evokes Reflection: Learning Efficiency in Spatial Visualization
Glenn
Gordon Smith, State University of New York at Stony Brook
About
the author...
Abstract
Different levels
of interaction in a computer game-like situation were compared as a means of
learning efficiency on an internet-based spatial visualization task, involving
polyomino puzzles. 109 undergraduates were divided among three treatment groups:
pilots, who interactively attempted to solve the puzzles; consultants, who watched
and talked with pilots without interacting; and copilots, who alternated between
pilot and consultant roles every 40 seconds, and collaborated. Participants
were tested before and after engaging in the experiment. Repeated measures analyses
showed pilots and copilots learned more than consultants. Differences were significant
at 0.05. Copilots learned most. These results suggest that alternating between
interaction and observation is the best way to learn spatial visualization.
1. Introduction
With the proliferation of interactive computer environments, such as simulations,
tutorials and "edutainment," in a variety of highly spatial content
areas such as math (especially geometry), chemistry, and physics, it is important
to investigate the relationship between hands-on interaction with computer programs
and the acquisition of spatial visualization skills. Typically educational situations
involve both hands-on and observational activities. For example, in a math class,
students might first watch the teacher solve problems on the board, then attempt
to solve problems themselves. Similarly in a class on Excel, students might
first watch the teacher create spreadsheets and then create spreadsheets themselves.
Cooperative learning groups in school computer labs often place one student
at the mouse and keyboard with one or more other students watching and advising;
an alternate model of cooperative learning in computer labs has students taking
turns at the controls. The comparative effectiveness of different variations
of hands-on interactivity (hands-on, observation, taking turns, etc.) for learning
spatial visualization is an important issue for the pedagogy of computer-based
learning.
Although measurable by a number of standardized tests and accepted as a valid psychological construct, because of its non-verbal nature, spatial visualization remains elusive to unambiguous definition. I offer the following eclectic definition: Spatial visualization is the ability to solve multi-step problems involving configurations of shapes, primarily using mental imagery or other mental representations and transformations of same which explicitly preserve the topological and geometric relations of the problem, while optionally involving additional logical, verbal and symbolic reasoning.
Spatial visualization is an important factor in student success in a variety of spatial domains such as geometry (Battista, 1990), other higher forms of mathematics (Battista, 1990; Smith, 1964), chemistry (Pribyl & Bodner, 1987) and physics (Pallrand & Seeber, 1984).
Interestingly there is a relationship between time and spatial visualization. Without time pressure, people often resort to entirely non-spatial strategies for solving spatial problems (Smith, 1964). Moreover, the amount of elapsed time as well as success in solving the task provides a more accurate measure of spatial skill. If someone takes an exceedingly long time to solve a spatial problem, his/her success may be more indicative of patience or persistence than spatial visualization skill. For the purposes of measurement, it is more productive to record elapsed time, along with success rate, and determine spatial visualization efficiency as the success rate divided by elapsed time.
Additionally there is a relationship, long posited by scientists, between acquisition of spatial visualization skill and hands-on interaction. Piaget & Inhelder (1948) suggested that a combination of hands-on touching and integration of different viewpoints is instrumental in children's development of spatial ability and mental models of spatial objects. There are similar connections between spatial visualization and interaction with virtual shapes in computer programs. Interactive computer graphics can facilitate improvements in adolescents' and adults' spatial visualization (Okagaki and Frensch, 1994; Gagnon, 1985).
The principle of spatial weaning (Smith, 1998) suggests that hands-on, interactive situations may initially be more beneficial to novices to a spatial domain who may not be familiar enough with the geometry of that new spatial domain to construct the mental imagery necessary for visualizing solutions. Once students become more familiar with the geometry of the new domain, they may benefit more from less interactive situations. They are now familiar enough with the geometry of that domain to construct the mental imagery necessary to visualize hypothetical solutions without the scaffolding of hands-on stimuli.
However, the very opposite of hands-on interaction, i.e., relatively more passive observation, sometimes has the advantage in educational settings (Sweller, 1994). Hands-on manipulation may divert short -term memory resources needed for students to comprehend a new schema requiring the simultaneous mental manipulation of a larger number of elements. When algebra or geometry students are learning specific principles or techniques, it is often more beneficial for them to observe the teacher working on a problem than to immediately try to solve it themselves. Immediately solving problems by applying principles only recently introduced imposes an extraneous "cognitive load" on the students' short-term memory (Sweller, 1994). As students mentally manipulate the elements of the problem, they must also hold in mind the new principle that the problem illustrates, straining the capacity of their short term memory.
Considering that there are theoretical advantages for both interaction and observation, an important question is 'How do interaction versus observation compare as learning situations?' Smith (1998) provided some evidence that fifth-grade students, less skilled in spatial visualization, benefit more from computer interaction, while fifth-graders already skilled in spatial visualization benefit more from observation. However, it is unclear how these results extend to other age groups and other learning situations. Moreover, it is unclear how alternating between interaction and observation, another possible variation of spatial weaning, might affect acquisition of spatial visualization skills. These questions have important implications for the pedagogy of interactive computer programs in a variety of subjects involving spatial visualization skills, such as geometry, chemistry, physics, etc.
The current study seeks to statistically test the principle of spatial weaning discovered with think-aloud methods on fifth graders (Smith, 1998) and extend it to another age group, i.e., college undergraduates. Spatial weaning predicts that students unfamiliar with a spatial domain will benefit most from high interaction, while benefiting least from observation alone.
Furthermore, we are interested in looking at these concepts from the point of efficiency in spatial visualization. Timed spatial tests emphasize mental imagery and provide a more accurate measure of spatial visualization skill than tests with no time limits. Therefore we are interested in efficiency in spatial visualization, i.e., how many problems can be solved divided by average time to solve them.
Our main research question is: How do a) hands-on interaction and b) observation compare as collaborative computer-based situations for learning efficiency in spatial visualization?
Since the pedagogy of computer interaction and spatial visualization is relatively new, a broader search of learning conditions is warranted. Perhaps some variation of hands-on interaction might be most beneficial. Thus we examined another variation on spatial weaning, i.e., alternating between interaction and observation/consulting. A secondary research question focuses on variations in hands-on interaction with a computer: How do a) exclusively hands-on interaction, b) intermittent hands-on interaction (alternating between hands-on and observation) and c) observation compare as learning situations for efficiency in spatial visualization?
2. The Study
The study used polyomino puzzles because they require a variety of spatial
visualization skills, such as mental rotation, that are often used in solving
geometry problems. 109 college undergraduates (48 male, 61 female, mean age
18.3 years) solved two types of computer-based polyomino puzzles: 'I-puzzles':
Interactive puzzles, where participants drag and rotate pieces via mouse to
assemble them into a target shape (see figure 1), and 'M-puzzles': multiple
choice static 'visualization puzzles' where pieces cannot be moved, but participants
must use spatial visualization to determine which of four static puzzles could
be hypothetically solved (see figure 2). Validity of the M-puzzles as a measure
of spatial visualization was previously obtained through correlation (.518)
with a standardized test of spatial visualization, the Differential Aptitude
Test, Space Relations Subset (DAT, authored by Bennett, Seashore, & Wesman,
1947).

Figure 1. An I-puzzle.
![]() An interactive demo of an I-puzzle.
An interactive demo of an I-puzzle.
Require Java-enabled browser.
Beginning position of an I-puzzle: the shapes on the left can be dragged and
rotated by mouse to assemble the shapes into the shape on the right. Ending
position of an I-puzzle: the smaller shapes have been assembled onto the larger
shape. classified as a solved I-puzzle.
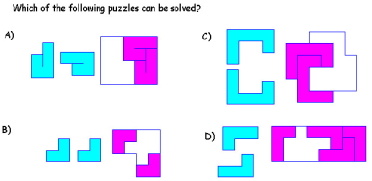
Figure 2. An M-puzzle.
The participant must pick which puzzle could be solved without
removing the shapes already on the larger target shape.
In both types of puzzles, mirroring (or reflection) was not an allowed transformation. This created situations where the students had to mentally rotate shapes accurately to determine if a shape and a space it might hypothetically be placed in were congruent. If a hypothetical solution required a reflection, obviously it was not valid.
The M-puzzles and I-puzzles are complementary, using the same types of shapes. The M-puzzles are designed as a test of spatial visualization. The I-puzzles are intended as an interactive activity to exercise and improve spatial visualization and thus performance on the M-puzzles.
The experiment employed a pre-test, treatment, post-test design. Pre-test and post-test each consisted of 9 randomly ordered M-puzzles presented to the participants by a web-browser over the internet via a Javascript program, with the results being written back to the server machine. Elapsed times were recorded locally on the computers used. Only when a participant finished the entire set of puzzles, was the data sent over the internet. Thus there was no issue of inaccuracies as a result of internet lag.
The pre-test and the post-test are approximately equal in difficulty, the M-puzzles having been calibrated at an earlier period. The M-puzzles were partitioned into two groups (pre-test and post-test) of approximately equal difficulty.
Participants were specifically instructed, in writing and orally, that time was a factor and they should solve the M-puzzles as quickly but as accurately as possible.
On the M-puzzles used in the pre-test and post-test, participants received feedback, after each puzzle, as to whether they answered it correctly. After the full set of puzzles was completed, they were told how many they answered correctly and were given a whimsical ranking, such as "Space Cadet," "Sargent," or "Master-at-Arms," dependent on the number correct. Thus participants were able to monitor their progress from pre-test to post-test. The pre-test and post-test were completely individual activities. Participants were not allowed to talk or otherwise collaborate with each other in any way during pre-test and post-test. Because the M-puzzles were presented in a different random order to each participant, opportunities for copying from each other were minimal.
In order to isolate and analyze the effects of high and low active control during the treatment, two thirds of the participants were "yoked" together in "pilot-consultant" pairs. The pilot interactively solved as many, progressively harder, I-puzzles as possible within a 40 minute period. The consultant sat next to the pilot, in front of the same computer, and watched the pilot solve the I-puzzles, but was unable to interact in a hands-on manner (via mouse or any other input device) with the computer display. However the consultant was instructed to pay close attention to the pilot's progress on the I-puzzles. The pilot and consultants were instructed to talk with each other as a collaborative team working towards the common goal of solving as many puzzles as possible within the 40-minute period. The pilot and consultant scenario just described represented two of the three treatment conditions.
For the third treatment condition, referred to as the copilot condition, pairs of participants alternated every 40 seconds between being pilot and consultant. In the copilot pairs, two people, via two mice, were connected to one computer. A switching device, known as the Siamese Twin Computer Mouse (patent pending), allowed only one of the mice at a time to be active and automatically switched which mouse was active every 40 seconds. See figure 3.

Figure 3. Siamese twin Computer Mouse.
Thus for 40 seconds, one participant had interactive control over the I-puzzles, while another participant paired with him/her watched the same visual display without being able to interact with the mouse. The next 40 seconds, the roles were reversed so that the participant last observing now had interactive control, and vice-versa. LED's positioned on top of the monitors alerted participants of their current role. A lit LED indicated interactive control, while an unlit LED indicated observation. Copilot pairs were instructed to talk with each other and work towards the common goal of solving as many of the progressively harder I-puzzles as possible during the 40-minute period.
All participants, pilots, consultants and copilots were explicitly instructed to talk, collaboratively, with their partner during the treatment and to learn as much as possible from the treatment because this knowledge would be useful for the post-test. The pre-test and post-test data from the three groups, pilots (39), copilots (36), and consultants (34), provided data focusing on the secondary research question: " How do a) exclusively hands-on interaction, b) intermittent hands-on interaction (alternating between hands-on and observation) and c) observation compare as learning situations for efficiency in spatial visualization? "
With the experimental design used, approximately two-thirds (or 75) of the participants (pilots and copilots) were "hands-on," experiencing a significant amount of interaction with the computer during the treatment. Approximately one-third (or 34) of the participants were "consultants," experiencing no direct interaction with the computer. The pre-test and post-test data, grouped by hands-on versus consultants, provided data for answering the main research question, "How do a) hands-on interaction and b) observation compare as collaborative computer-based situations for learning efficiency in spatial visualization?"
3. Findings
As a baseline to determine if learning took place on average for all the participants,
pre-test to post-test progress in efficiency was analyzed with an F-Test of
Multiple µ's. The test was significant at alpha = 0.05, F-Ratio = 4.68, with
an obtained significance level of 0.032. Mean of pre-test efficiency was 0.0798,
while for post-test the mean was 0.0972. Standard deviations for pre-test and
post-test were 0.0556 and 0.0628 respectively.
To investigate the main research question, how hands-on versus observation compare for learning of efficiency of spatial visualization, repeated measures analyses were used. One analysis of variance, with repeated measures of efficiency on pre-test and post-test as the dependent variable, and with independent grouping variable hands-on versus consultant, and gender as covariant, was significant at the 0.05 level (F = 3.98, obtained significance level was .049). Table 1 shows the means for the efficiency for the two groups (hands-on versus consultants) in pre-test and post-test.
| Hands-on | Consulting | |
| Pre-test | 0.0807 | 0.0779 |
| Post-test | 0.104 | 0.0817 |
Table 1. Means of efficiency by group, hands-on and consulting.
Table 2 shows the means of efficiencies on the pre-test and post-test for the three groups, pilot, copilot and consultant.
| Pilots | Copilots | Consultants | |
| Pre-test | 0.0811 | 0.0802 | 0.0779 |
| Post-test | 0.102 | 0.107 | 0.0817 |
Table 2. Means of efficiency by group, pilots, copilots and consultants.
Note that the copilot group had the highest post-test mean efficiency, as well as the most improvement in efficiency from pre-test to post-test, while the consultant group had the lowest in both. The results for the pilots group were similar to that of the copilots. A second repeated measures, focusing on copilots and consultants only, with efficiency as the dependent variable and role as the independent variable, was also significant at the 0.05 level (F=5.861, level of significance obtained was 0.018. A third repeated measures analysis of pre-test and post-test efficiency, looking at the pilots and the consultants only, and also with gender as a covariate, was not significant at the 0.05 level (F=1.886, obtained significance was 0.174).
To investigate the secondary research question, how exclusively hands-on (pilots) versus intermittent hands-on (copilots) compare for learning efficiency in spatial visualization, we compared how the two interactive groups (pilots and copilots) progressed, pre-test and post-test, in terms of efficiency. Selecting only the groups, pilots and copilots, a repeated measure of pre-test and post-test efficiency, with grouping variable role during the treatment (pilot versus copilot) and gender as covariant, was not significant at the 0.05 level. F was .357.
4. Conclusions
Since across all the participants,
the post-test mean of efficiency was significantly greater than the pre-test,
learning of spatial visualization apparently occurred. The experiment provided
an appropriate scenario for comparing different situations for learning spatial
visualization.
We can also conclude that some amount of interaction with the computer is superior to no interaction, since the repeated measures analysis, comparing hands-on (pilots and copilots) versus consultants, indicated a significant difference in improvement on efficiency in spatial visualization. Similarly intermittent interaction with a computer is clearly preferable to consulting/observing, since the repeated measure analysis comparing the copilot and consultant groups indicated a significant difference. On the other hand, there was no significant difference in learning between exclusive interaction with a computer and intermittent interaction.
The first theoretical constructs
motivating this study was spatial weaning, the idea that hands-on/interactive
situations may be initially more beneficial to novices to a spatial domain
(system of shapes) than hands-off/reflective situations. The additional sense
information, the integrated visual, tactile, proprioceptive and motor processes
associated with the hand-eye coordination of interactively solving spatial problems,
provides a scaffolding for learning mental image-based transformations, such
as mental rotation, particular to that spatial domain (system of shapes).
The results indicate that the principle of spatial weaning, discovered in the
context of young children, applies as well to adults. That the copilot/alternating
group performed best indicates that length of time period needed for spatial
weaning is relatively short for college students. Hands-on/interactive situations
provide additional advantages such as involvement, greater attention and motivation.
The second theoretical construct motivating this study was cognitive load, or
the idea that hands-on interaction may impose an extraneous cognitive load that
interferes with learning of the new skills. Cognitive load theory predicts that
the consultant group should outperform the two hands-on groups, but this was
definitely not the case in this experiment. This is especially surprising considering
that the consultant treatment condition was much more similar to the post-test
than was either of the hands-on conditions. Since both the consultant and post-test
activities were hands-off and reflective, one might have expected optimal transfer.
However, since the copilot (or alternating) group learned most, perhaps periodic
role-switching promotes meta-cognition, or productive reflection on the problem-solving
process, i.e., interaction evokes reflection. Hands-on and consulting are complementary.
Both spatial weaning and cognitive load theory are supported by the results.
The recommendation for teachers is to have their students alternate interactive activities with more reflective activities. In terms of classroom logistics, when pairing-up students on computers, intermittent interaction via the Siamese Twin mouse, provides twice as many students with hands-on interactive experience, than is possible with an exclusive hands-on situation.
5. References
Battista, M. T. (1990). Spatial visualization and gender differences in high
school geometry. Journal of Research in Mathematics Education, 21(11), 47-60.
Bennett, G. K., Seashore, H. G., & Wesman, A. G. (1972). Differential aptitude tests: Space relations (Form A). New York: Psychological Corporation.
Gagnon, D. (1985, Winter). Videogames and spatial skills: An Exploratory Study. Educational Computing Technology Journal, 33(4), 263-275.
Okagaki, L., & Frensch, P. A. (1994). Effects of video game playing on measures of spatial performance: Gender effects in late adolescence. Journal of Applied Developmental Psychology, 15(1), 33-58.
Pallrand, G. J. & Seeber, F. (1984). Spatial ability and achievement in introductory physics. Journal of Research in Science Teaching. 21, 507-516.
Piaget, J. & Inhelder, B. (1948). The Child's Conception of Space. New York, N.Y.: W. W. Norton & Co.
Pribyl, J. R. & Bodner, G.M. (1987). Spatial ability and its role in organic chemistry: A study of four organic courses. Journal of Research in Science Teaching, 24, 229-240
Smith, I. M. (1964). Spatial Ability: Its Educational and Social Significance. San Diego, CA: Robert R. Knapp.
Smith, G. G. (1998). Computers, computers games, active control and spatial visualization, strategy. Unpublished Ph.D. dissertation, Arizona State University, Tempe, Arizona.
Sweller, J. (1994). Cognitive load theory, learning difficulty, and instructional design. Learning and Instruction, 4(5), 295-312.
********** End of Document **********
| IMEJ multimedia team member assigned to this paper | Yue-Ling Wong |