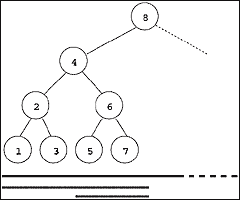
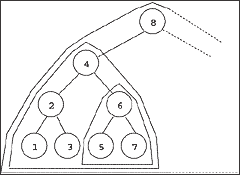
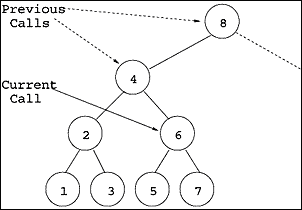
Animating Recursive Algorithms
Linda Stern, The University of Melbourne
Lee Naish, The University of Melbourne
Abstract
Designing visual representations for recursive algorithms has been addressed
within a pedagogically-oriented framework for animating algorithms. We
present a classification for choosing the kind of visual representation
that is most helpful to students. The classification is based on the way
the algorithm navigates through a data structure and manipulates data
items within a data structure, and suggest strategies for visual representation
that work within the categories of this classification. Further opportunities
for tailoring representation derive from the shape of the data structure
and particular forms of recursion, such as tail recursion. While there
may be no single, general way to represent recursive algorithms, our classification
is a
useful guide to picking an appropriate strategy for use when animating
recursive algorithms for teaching purposes.
1. Introduction
The Algorithms in Action (AIA) project [14] uses multimedia animations
of algorithms as a pedagogical tool to help students learn. Our target
group of students is studying a second-year core curriculum subject on
data structures and algorithms, where the concentration is on searching
and sorting algorithms. The students are familiar with the concept of
recursion, but have not yet been exposed to any but the simplest of algorithms.
Although several algorithm animations are available, especially for the simpler algorithms [4], few satisfied our need for pedagogically oriented animation. Notable exceptions are Gloor's CD companion [7] to a text on algorithms [5] and the collaborative active textbooks of Marc Brown [2, 3], neither of which fit well with our syllabus and choice of textbook [11].
Our aim in developing AIA was to find a general approach to presenting and animating algorithms and to implement a framework that could be used as the basis for presenting specific algorithms. The expectation was that interactive visual presentation would help students develop both an overall conceptual idea of how each algorithm works and a more detailed procedural understanding.
2. The Algorithms
in Action Framework
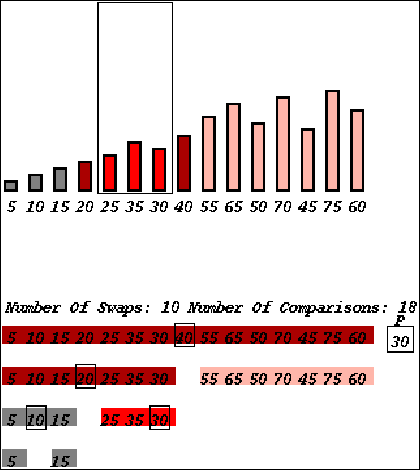
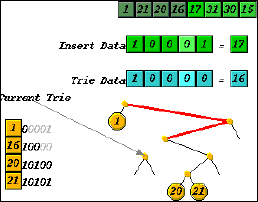
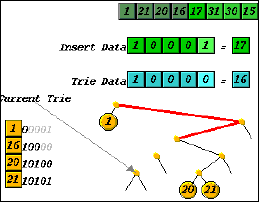
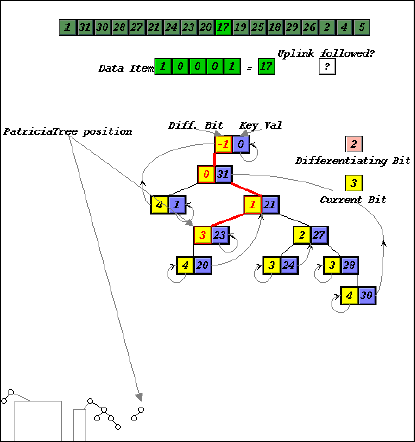
The AIA framework consists of animation, pseudocode, and textual explanation,
all coordinated, as previously reported [15]. A cursor traces the execution
of the algorithm through pseudocode, while the animation displays a conceptual
representation of each step. Students control the level of detail being
displayed by expanding or contracting lines of pseudocode. At higher levels
of abstraction the animation helps students to grasp the overall concept
of an algorithm, while the more detailed views help them understand the
workings of the algorithm at a procedural level. The level of detail in
the animation, in the explanation, and in the pseudocode expand and contract
synchronously.