
Animating
Recursive Algorithms
Linda
Stern, The University of Melbourne
Lee Naish, The University of Melbourne
Abstract
Designing visual representations for recursive algorithms has been addressed
within a pedagogically-oriented framework for animating algorithms. We present
a classification for choosing the kind of visual representation that is most
helpful to students. The classification is based on the way the algorithm navigates
through a data structure and manipulates data items within a data structure,
and suggest strategies for visual representation that work within the categories
of this classification. Further opportunities for tailoring representation derive
from the shape of the data structure and particular forms of recursion, such
as tail recursion. While there may be no single, general way to represent recursive
algorithms, our classification is a useful guide to picking an appropriate strategy
for use when animating recursive algorithms for teaching purposes.
1. Introduction
The Algorithms in Action (AIA) project [14] uses multimedia animations of algorithms
as a pedagogical tool to help students learn. Our target group of students is
studying a second-year core curriculum subject on data structures and algorithms,
where the concentration is on searching and sorting algorithms. The students
are familiar with the concept of recursion, but have not yet been exposed to
any but the simplest of algorithms.
Although several algorithm animations are available, especially for the simpler algorithms [4], few satisfied our need for pedagogically oriented animation. Notable exceptions are Gloor's CD companion [7] to a text on algorithms [5] and the collaborative active textbooks of Marc Brown [2, 3], neither of which fit well with our syllabus and choice of textbook [11].
Our aim in developing AIA was to find a general approach to presenting and animating algorithms and to implement a framework that could be used as the basis for presenting specific algorithms. The expectation was that interactive visual presentation would help students develop both an overall conceptual idea of how each algorithm works and a more detailed procedural understanding.
2. The Algorithms in
Action Framework
The AIA framework consists of animation, pseudocode, and textual explanation,
all coordinated, as previously reported [15]. A cursor traces the execution
of the algorithm through pseudocode, while the animation displays a conceptual
representation of each step. Students control the level of detail being displayed
by expanding or contracting lines of pseudocode. At higher levels of abstraction
the animation helps students to grasp the overall concept of an algorithm, while
the more detailed views help them understand the workings of the algorithm at
a procedural level. The level of detail in the animation, in the explanation,
and in the pseudocode expand and contract synchronously.
3. Recursion
Representing recursive algorithms in ways that will be helpful to students has
proven to be more challenging than designing representations for iterative algorithms.
While initially we sought a general approach to the problem of displaying recursive
algorithm, in practice, we found that the choice of most suitable representation
depended on the particular algorithm being displayed.
The most appropriate visual representation for recursive algorithms was correlated with a classification based on how the algorithm navigates through and manipulates the data items within the data structure [13]. In this classification, one category of algorithms consists of those that traverse a static data structure (e.g. search), another category contains algorithms that manipulate items within an existing data structure (e.g. sort), and a third category contains algorithms that build a data structure (e.g. insert). Within these categories, it was sometimes useful to further subdivide based on additional criteria, such as tail recursiveness and data structure shape.
4. Code Tracing of Recursive
Calls
In AIA, only one copy of the recursive function is shown in the pseudocode.
As a recursive call is made, the pseudocode tracing restarts at the top of the
function. Visual clues assist with clarity here, and most of our second-year
students understand that when the pseudocode cursor jumps from the recursive
call within the function to the top of the same function, this represents a
new function call. This approach might not be suitable for beginning programmers,
where it may be useful to pop up a new window for each recursive call [16].
5. Recursive Manipulation
of Data Items within an Existing Linear Data Structure
In recursive sorting algorithms, such as quicksort and merge sort, the starting
point is an array or linked list containing the data items to be sorted. The
data structures are linear, and the algorithms use the classical divide-and-conquer
approach, where the algorithm makes a number of recursive function calls to
smaller and smaller parts of the data structure. During each recursive call,
some data items are rearranged. For example, in quicksort, each function call
partitions the data such that all items before a designated "pivot"
element are smaller than (or equal to) the pivot, and all items after are larger
(or equal). Two recursive calls are then made, one to the part of the array
with the smaller elements, and another to the part of the array with the larger
elements. The student's task is to learn what happens during each recursive
call and to understand how the progression of recursive calls moves the sorting
process through the data structure.
For these algorithms, where data items within an existing linear data structure are manipulated without the data structure changing its size or shape, we represent each recursive call by a horizontal line under the sequence of data items referred to in the recursive call (Figure 1). The value of each data item is represented by a vertical bar, similar to the representation used in the seminal algorithm animation video, "Sorting out Sorting" [1]. Our use of horizontal bars to underline the segment of the data structure being manipulated during the recursive call bears a similarity to the design used by Dershem and Brummond [6]. Additionally, different shades of color distinguish between the currently active call, calls on the function stack, and completed calls.
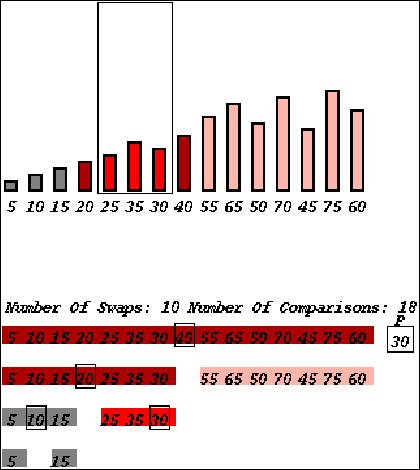
Figure 1. Quicksort animation, showing recursive calls. The current recursive call is sorting the elements 25, 35, 30, with 30 as the pivot (shown by the box). Elements up to 20 have already been sorted, while elements from 40 onwards are waiting for a call on the stack to be done.
6. Recursive Navigation
through a Linear Data Structure
Searching through a dictionary abstract data type entails navigating through
a data structure, searching for a data item with a particular key. Initially
nothing is known about the location of the key. As the search progresses the
subset of possible locations is narrowed down.
Where the data structure is linear, navigation can be represented by horizontal lines under the data items referred to in the recursive call. This is similar to the representation used for quicksort, except that the search narrows in scope as it progresses (Figure 2), since there is only one recursive call, instead of the two recursive calls made by each invocation of quicksort.
This representation can also be useful for an equivalent iterative coding as it gives the history of the search at a single glance, but is less natural.
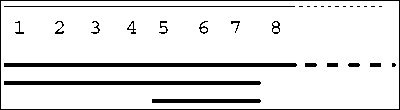
Figure 2. Binary search, showing 3 recursive calls. The horizontal lines under the data structure show subarrays for successive recursive calls.
7. Navigation and Data
Manipulation in Non-linear Data Structures
Data structures for search often have a nonlinear tree structure, which makes
visualizing the current subset of the data more challenging. For a tree structure,
there are several different ways in which the current subtree can be shown.
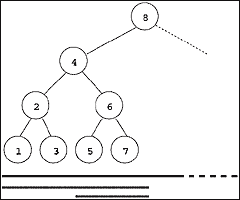
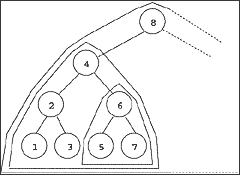
Given some constraints on the tree layout, a horizontal bar similar to the horizontal
bars used in quicksort can underline the leaves of the current subtree (Figure
3a). Alternatively, a modified approach can enclose subtrees involved in recursive
calls in polygons (Figure 3b). Less abstractly, a pointer to the root of the
subtree can be shown (Figure 3c).
The choice of representation is influenced by the students' background. First year students might find it easiest to understand the algorithm where the entire subtree is outlined. Later year students would generally be able to understand the significance of a pointer to the root of the subtree. The pointer representation has the advantage of being closest to the recursive code, and students might find this representation assists them in following the pseudocode closely. The pointer representation, alone or in combination with other representations, may help students make the link between the algorithm code and progression through the data structure, conceptualizing the idea that the subtree whose root is being pointed to consists of all the data still under consideration. Horizontal bars under the data structure might be useful in cases where the data structure is complicated and an objective is to reduce clutter on the screen, and can highlight the similarities between different algorithms, such as searching a (balanced) binary search tree (Figure 3a) and binary search in an array containing the inorder traversal of the same tree (Figure 2).
 (a)
(a)
 (b)
(b)
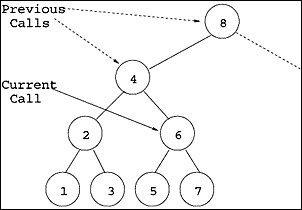 (c)
(c)
Figure 3. Recursive
binary search tree, showing three different ways to display the part of the
data involved in the current recursive call:
(a) The leaves, or outer extent, of the current tree are underlined;
(b) Polygons are used to outline the subtree under investigation, with
larger triangles showing the history of previous recursive calls;
(c) A pointer to the root of the subtree corresponding to the current
recursive call is shown (solid line arrow); optionally, a history of recursive
calls can be kept (dotted line arrows).
8. Navigation Using Non-Tail
Recursive Algorithms
Where code is tail recursive, the currently active function call narrows the
search one step, while the rest of the searching is done in successive recursive
calls. The tail recursive algorithm is very similar to an iterative while loop.
Visual representation for both recursive and iterative codings must indicate
which part of the data structure is under investigation. For a recursive implementation,
it is natural for the display to indicate multiple subsets of the data, getting
smaller as the search progresses through multiple recursive calls.
When the code is not tail recursive, there is work to be done upon returning from the recursive call. The location of the recursive call within the code is important because it determines what work is to be done upon return from the call. The pedagogical challenge here is to help students keep track of the point in the calling function where the recursive call is made, as well as how the navigation is progressing through the data structure.
For example, when navigating through a splay tree [11] "rotations" are performed after the return from the recursive call. Rotations are local operations on a small portion of the tree, intended to improve the overall balance of the tree. Because the place of the rotations within the algorithm may not be immediately obvious to a student just learning the algorithm, we supplement the main animation display with an abbreviated function stack (Figure 4). The aim of showing the function stack is to track the progress through the calling function, and to show the work still to be done after return from the recursive call. We are, in effect, combining two types of animation: animating the result of the program, in the tree, and simultaneously animating the state of the program in the function stack [8], to help students make the mental link between the two processes.
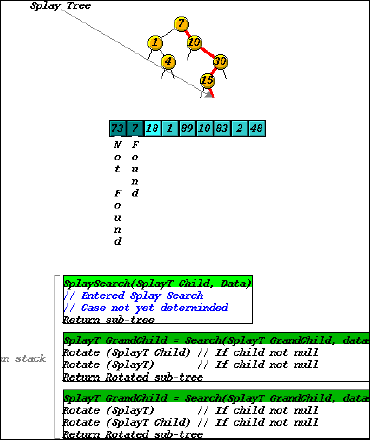 (a)
(a)
 (b)
(b)
Figure 4. Splay tree
search showing stack.
In (a) the stack contains three function calls. The third (top) call
has been called from the first line in the second call (highlighted).
In (b), the third call has returned, and the second call is performing
the rotation specified in its second line (now highlighted).
9. Recursive Insertion
into a Data Structure
Unlike navigation, which works on an existing data structure, insertion of items
into a data structure involves major changes in the size and possibly the shape
of the data structure. Accurate visual representation of recursive insertion
requires depicting changes in the data structure both during the growth phase,
when the correct insertion point is sought and recursive calls are added to
the function stack, and during the shrinking phase, when the recursive calls
return, the function stack shrinks, and the appropriate links within the data
structure are made.
For relatively uncomplicated algorithms, representation can be straightforward. Taking the radix search trie as an example, insertion involves creation of one new external node and possibly one or more internal nodes, which must all be linked into the trie. In animating insertion here, we depict the growth stage of the algorithm, where decisions about the path and nodes are made, by tracing the path to the insertion point, leaving gaps for the links, which are still to be made. (Figure 5). During the shrinking phase of the insertion algorithm, the animation shows the links forming as the recursive calls return. Since the eventual shape of the subtree after insertion of the new data is not known at the time of the growth phase, the pointer representation is convenient.
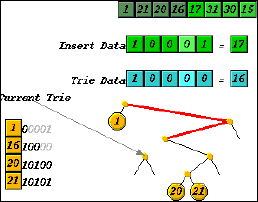 (a)
(a)
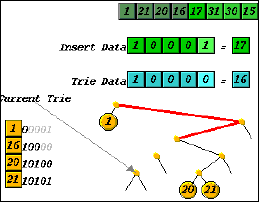 (b)
(b)
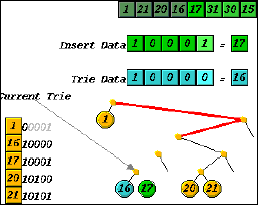 (c)
(c)
Figure 5. Insertion into radix trie. New nodes are formed as recursive calls are being made, but are not linked to the rest of the trie. The links will be made as the recursive calls return.
For more complicated algorithms, we supplement the main part of the animation with a thumbnail sketch that abstracts the data structure and indicates the part of the data structure referred to in the recursive call. For example, the main animation in our representation of a Patricia trie [11] shows all the details necessary to follow the workings of the algorithms, such as keys and upward links. Thumbnail sketches capture the essence, showing only nodes and links in the subtree currently being searched, without detail. The region to be searched by future recursive call(s) is represented by an large blank space (Figure 6). Thumbnail sketches are used in both the growth and shrinking phases of the algorithm, and are visually linked to the main animation. Over the course of the algorithm the thumbnail sketches allow us to build up a history of recursive calls, which helps students keep track of the overall progress of the recursive navigation.
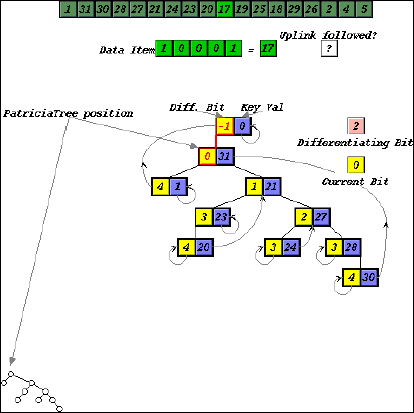 (a)
(a)
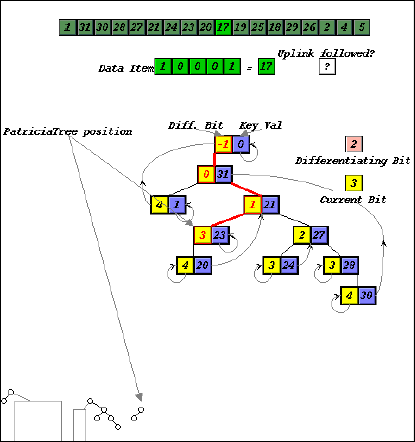 (b)
(b)
 (c)
(c)
Figure 6. Insertion into Patricia tree, with thumbnail sketches as navigation aids.
10. Evaluation
Our evaluation of the effectiveness of AIA has so far concentrated on the ways
in which students find the tool useful in their learning. To date we have not
specifically evaluated how students learn recursive algorithms, as distinct
from and how they learn iterative algorithms. Data has been derived from diverse
sources, including detailed usage logs, questionnaires, controlled observation,
and focus groups. Our observations indicate that students believe that the tool
allows them to learn better and faster. Particularly telling was the automated
logging, which showed significant usage over the semester -- an average of around
30 sessions per student in the most recent semester (Figure 7). There was an
initial peak when the system was first introduced to the students and, quite
significantly, a large peak before the examination. The two troughs in the graphs
corresponded to project deadline, i.e. students are otherwise occupied. In the
week prior to the examination alone, there was an average of 8 sessions per
student. Students' perceptions that the tool helped them learn was apparently
translated into the action of using the tool for at least part of their study
time.
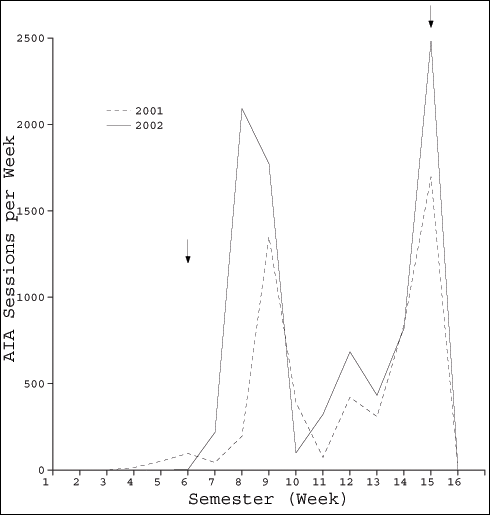
Figure 7. Usage of Algorithms in Action. Logging was done automatically during semester 1, 2001 and and semester 1, 2002. Numbers along the x-axis indicate teaching weeks, 1 being the first week of the semester. The y-axis shows the number of student sessions with AIA initiated during that week. Students can use multiple modules within a single session. Arrows indicate when Algorithms in Action was introduced to the class (week 5), and the week of the examination (week 15). Class size was approximately 300 students in both years..
Our initial intention was for students to use AIA in a top-down manner, first viewing algorithms at a more abstract level then increasing the level of detail (stepwise refinement). However, controlled observation revealed that some students used AIA in a bottom-up way, first expanding the pseudocode to give maximum detail then progressively contracting it as parts were understood. Following this observation, we concluded that students will use the tool according to their personal preferences and learning styles. We included a feature that allows the algorithm's pseudocode to be completely expanded with one mouse click, to facilitate bottom-up learning.
Variations were also seen in the different use that students made of the textual explanations. During controlled observation, little use was made of the text, yet the detailed logging shows that some students make heavy use of the explanations. This may be due to different student preferences, but another possibility is that students are more reluctant to take the time to read text while being observed. Research of others suggests that textual explanations are essential for effective learning in algorithm animation systems [12, 9].
To date we have not performed specific evaluation of the ways recursion is visualized in AIA. Based on our more general evaluation, it seems likely that looking in depth at how students use the tool to learn recursive algorithms will reflect the variety of students' preferences and will also suggest further ways in which we can enhance the animation framework to support different styles of learning.
11. Recursive, Iterative
or Both?
Many algorithms can be implemented either recursively or iteratively. Because
teachers and books generally show students only one implementation, the distinction
between the algorithm at a very abstract level and its implementation is sometimes
lost. We have speculated that students may find it helpful to look at the iterative
version during the initial stages of learning an algorithm, then progress to
the recursive version, which generally requires more abstract thinking. In this
section we suggest a way in which stepwise refinement can be used to merge recursive
and iterative versions of algorithms to aid understanding. We hope to implement
and evaluate this idea in the future.
At higher levels of abstraction, with the pseudocode contracted, it is possible to describe many algorithms in an iterative style, even when they may be coded recursively. Lower levels, with more detail, can reveal whether recursion or an iterative looping construct is used. Combining multiple implementations at the highest levels would emphasize to the students that recursion and iteration are merely implementation strategies, a concept that students often miss.
As an example, we show an algorithm for red-black tree insertion. Red-black trees are a kind of balanced binary search tree. The insertion algorithm performs rotations, and also "splitting" operations, which manipulate data and determine what rotations are performed. Iterative insertion algorithms perform splitting and rotation as the tree is traversed from root to the leaf, where the data is eventually inserted [10], and can trivially be recoded as a tail recursive implementation, with the operations performed just before the recursive call. There are also left-recursive algorithms, where splitting and rotation are performed after the recursive calls return - effectively, as the tree is traversed from leaf back to root. Yet another alternative is middle-recursive [11], where splitting is performed during the traversal down to a leaf and rotation is performed during the upward traversal.
Figure 8a shows the algorithm pseudocode at a high level in an iterative style. Figure 8b gives a lower level, or expanded, view. The two for loops have been expanded to reveal that the code is actually middle-recursive. The pseudocode expansion also shows that adding data at a leaf is done via the previous recursive call. By emphasising the common elements between different algorithm variations, we hope the students will gain a deeper understanding of algorithms and the variety of ways they can be implemented.
 (a)
(a)
 (b)
(b)
Figure 8. Red-black
tree insertion:
(a) high level pseudocode, iterative;
(b) lower level pseudocode, recursive implementation, showing relationship
to iterative approach.
12. Conclusion
While designing animations to help elucidate recursive algorithms to students,
we found that some visual representations were more helpful than others. We
noticed a correlation between the kind of visual representation that is most
effective and the way data items are being manipulated in the data structure.
We group the algorithms we have animated into three categories: those that navigate
through an existing data structure; those that manipulate data items within
a data structure; and those that insert data items into a data structure. Typically,
a particular visual representation works well for different algorithms within
one of these categories. Further subdivisions into the type of data structure,
e.g. linear or non-linear, and the type of recursion, e.g. tail-recursive vs.
non-tail-recursive, are useful in some instances. The choice among alternatives
is sometimes dictated by the level of the students and the pedagogical aims.
Given the multiplicity of situations and the multiplicity of learning styles,
we suggest that there is no single "best" visual representation fo
recursive algorithms.
13. Availability
Demonstration modules are available at http://www.cs.mu.oz.au/aia. Further modules
are available for teaching purposes, on request.
![]() An external link to www.cs.mu.oz.au/aia
An external link to www.cs.mu.oz.au/aia
14. Acknowledgments
We would like to thank the Teaching and Learning (Multimedia Education Technologies)
Committee of The University of Melbourne for their generous financial support.
We wish to thank Ka-Chi Cheung, Andrew Graham, and Tim Witham for programming,
Vic Ciesielski for assistance with the figures, and numerous anonymous students
for their feedback on modules under development.
15. References
[1] Baecker, R. Sorting Out Sorting. University of Toronto, Morgan
Kaufmann, 1981.
[2] Brown, M., Najork, M., and Raisamo, R. A Java-based implementation of collaborative active textbooks. In VL97: Proceedings of the IEEE International Symposium on Visual Languages (1997), pp. 372-379.
[3] Brown, M. H., and Najork, M. A. Collaborative active textbooks: A web-based algorithm animation system for an electronic classroom. SRC Research Report, Systems Research Center (1996).
[4] Brummond, P. The complete collection of algorithm animations. Last accessed at URL http://www.cs.hope.edu/~alganim/ccaa on 4 September 2001.
[5] Cormen, T., Leiserson, C., and Rivest, R. Introduction to Algorithms. MIT Press, 1990.
[6] Dershem, H., and Brummond, P. Tools for web-based sorting animation. SIGCSE Bulletin 30: Proceedings of the 29th SIGCSE Technical Symposium on Computer Science Education, 1 (1998), 222-226.
[7] Gloor, P., Dynes, S., and Lee, I. Animated algorithms: A hypermedia environment for "Introduction to Algorithms", MIT Press, 1993. ISBN 0-262-57096-3.
[8] Kann, C., Lindeman, R. W., and Heller, R. Integrating algorithm animation into a learning environment. Computers Educ. 28 (1997), 223-228.
[9] Naps, T., Eagan, J., and Norton, L. JAHVÉ - an environment to actively engage students in web-based algorithm visualization. SIGCSE Bull. 32 (2000), 109-113.
[10] Sedgewick, R. Algorithms in C, 2nd ed. Addison-Wesley, 1990.
[11] Sedgewick, R. Algorithms in C, Parts 1-4, 3rd ed. Addison-Wesley, 1998.
[12] Stasko, J., Badre, A., and Lewis, C. Do algorithm animations assist learning? an empirical study and analysis. In Proceedings of the INTERCHI '93 Conference on Human Factors in Computing Systems (Amsterdam, 1993), pp. 61-66.
[13] Stern, L., and Naish, L. Visual representations for recursive algorithms. In Proceedings of the 33rd SIGCSE Technical Symposium on Computer Science Education (Cincinnati, 2002), pp. 196-200.
[14] Stern, L., Naish, L., and Sondergaard, H. Algorithms in action. http://www.cs.mu.oz.au/aia.
[15] Stern, L., Søndergaard, H., and Naish, L. A strategy for managing content complexity in algorithm animation. In ITiCSE99: Proceedings of the Fourth Annual SIGCSE/SIGCUE Conference on Innovation and Technology in Computer Science Education (1999), pp. 127-130.
[16] Wilcocks, D., and Sanders, I. Animating recursion as an aid to instruction. Computers Educ. 23 (1994), 221-226.
********** End of Document
**********
| IMEJ multimedia team member assigned to this paper | Yue-Ling Wong |